
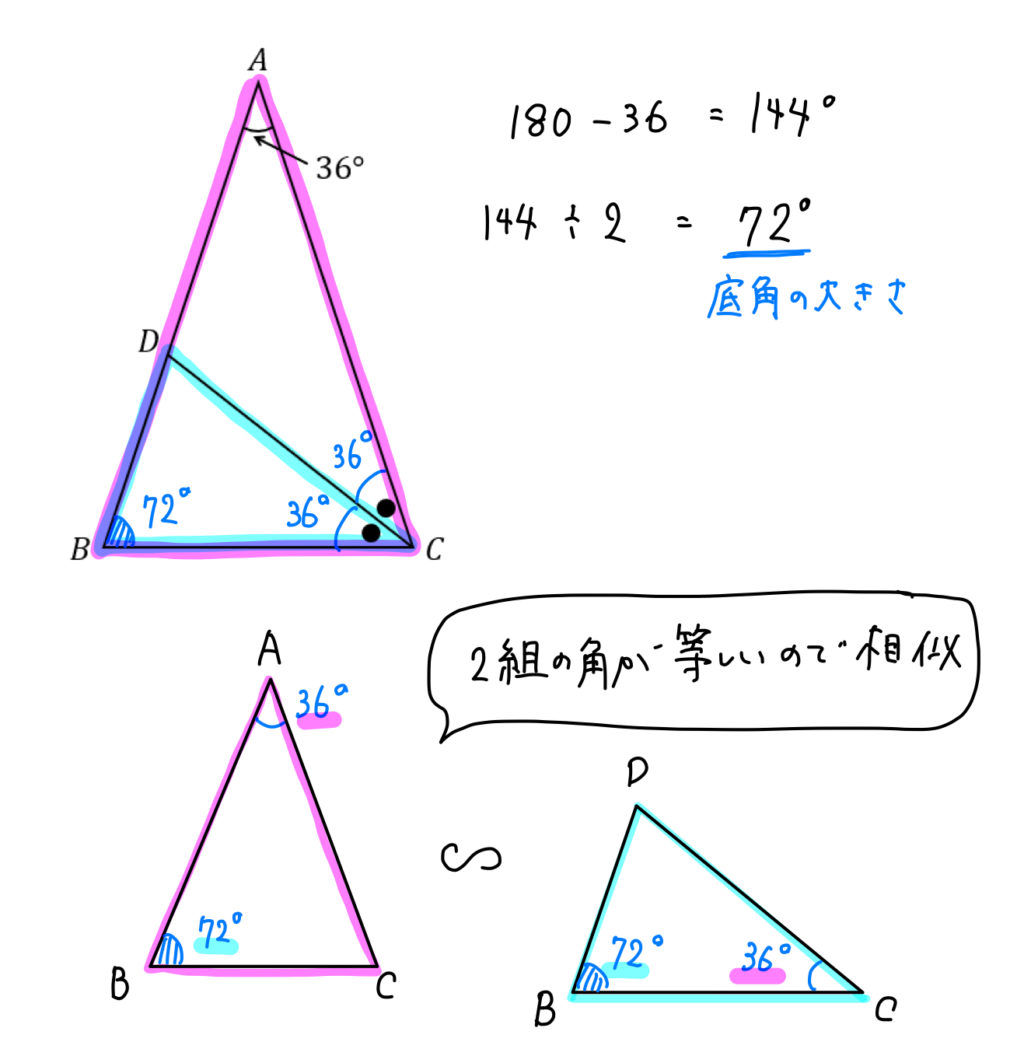
三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
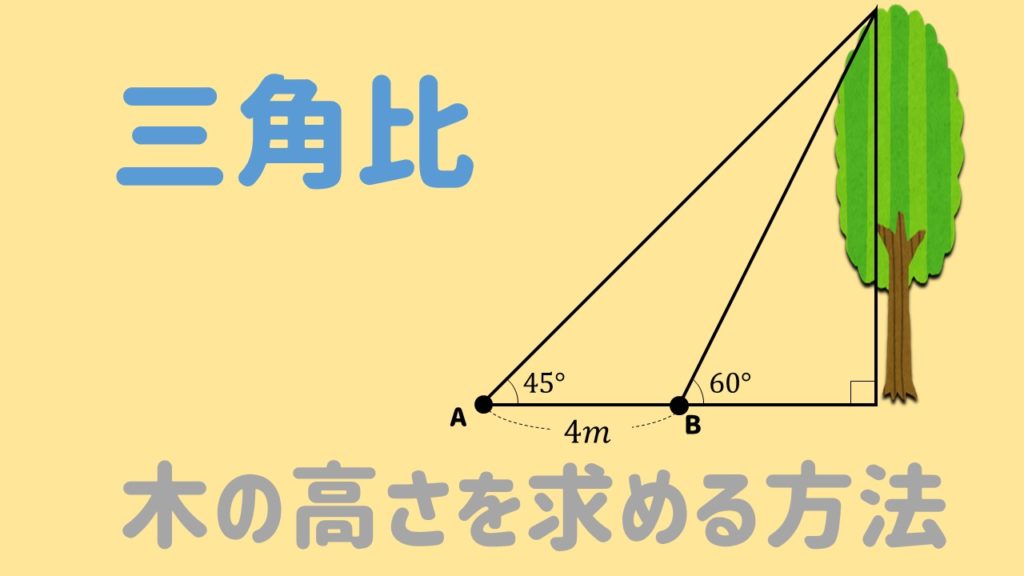
平行線と比の利用、辺の長さを求める問題をパターン別解説!←今回の記事 木の高さを求める方法について解説! 中点連結定理を使った問題を解説! 相似の面積比を求める問題をイチからやってみよう! 面積比!平行四辺形の面積問題を解説! 面積比!・直角三角形(斜辺と角度) 直角三角形の斜辺と角度から、底辺と高さと面積を計算します。 三角関数 ・角度から三角関数 角度(度またはラジアン)から三角関数を計算します。 ・三角関数から角度(逆三角関数) 三角関数から角度(逆三角関数)を計算します。
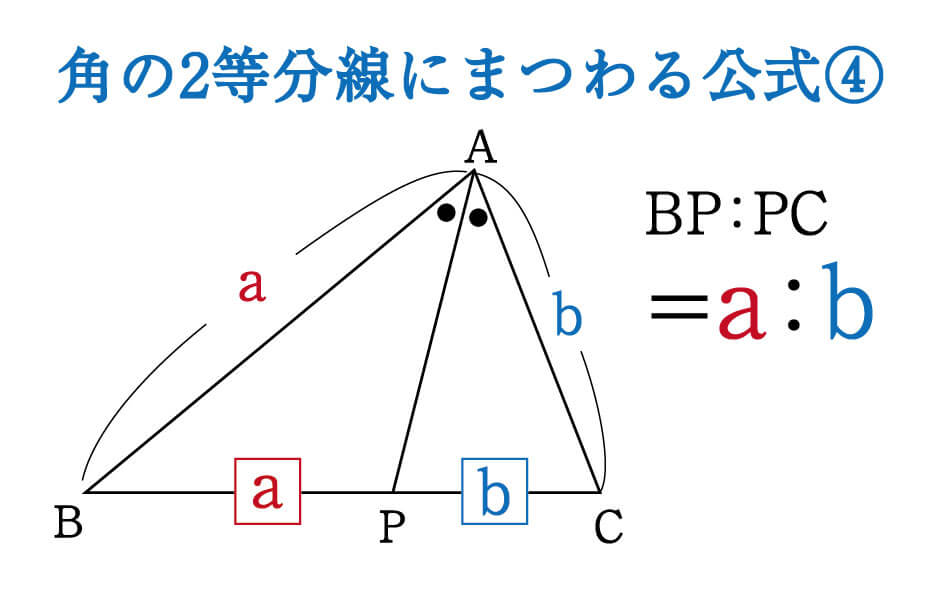
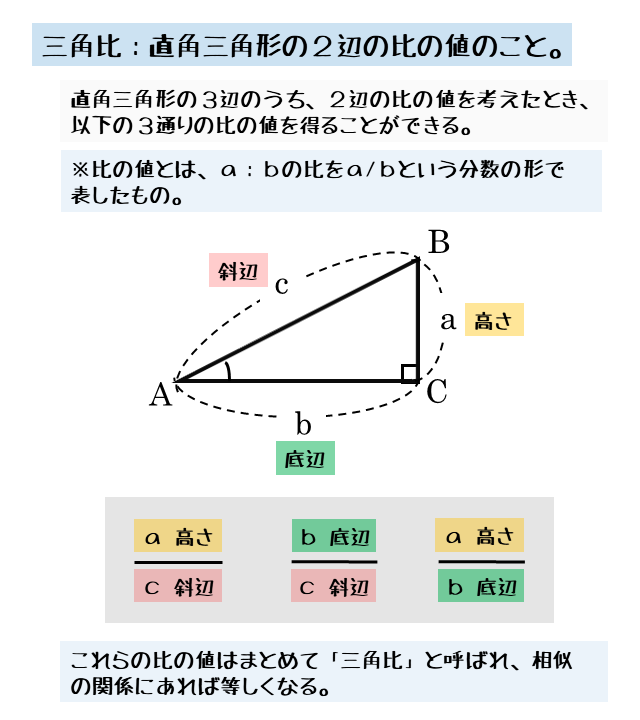
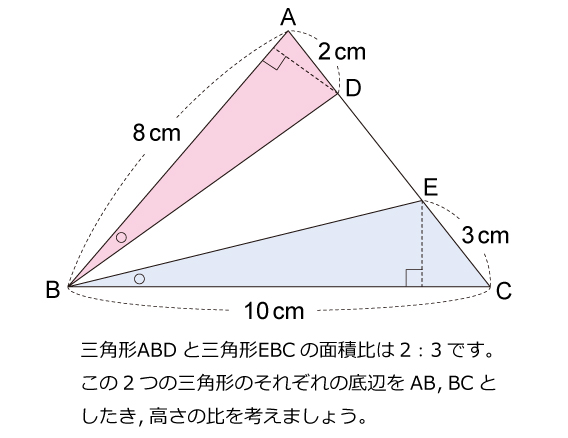
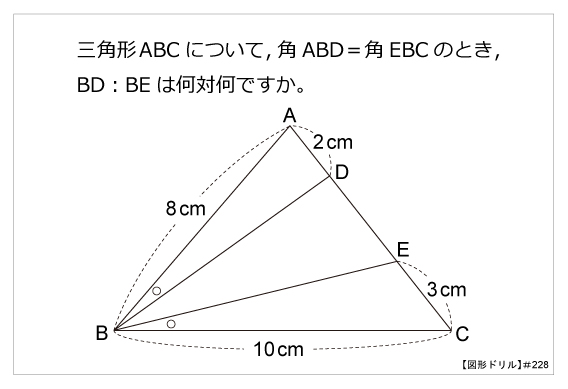
三角形 角度の比 辺の比
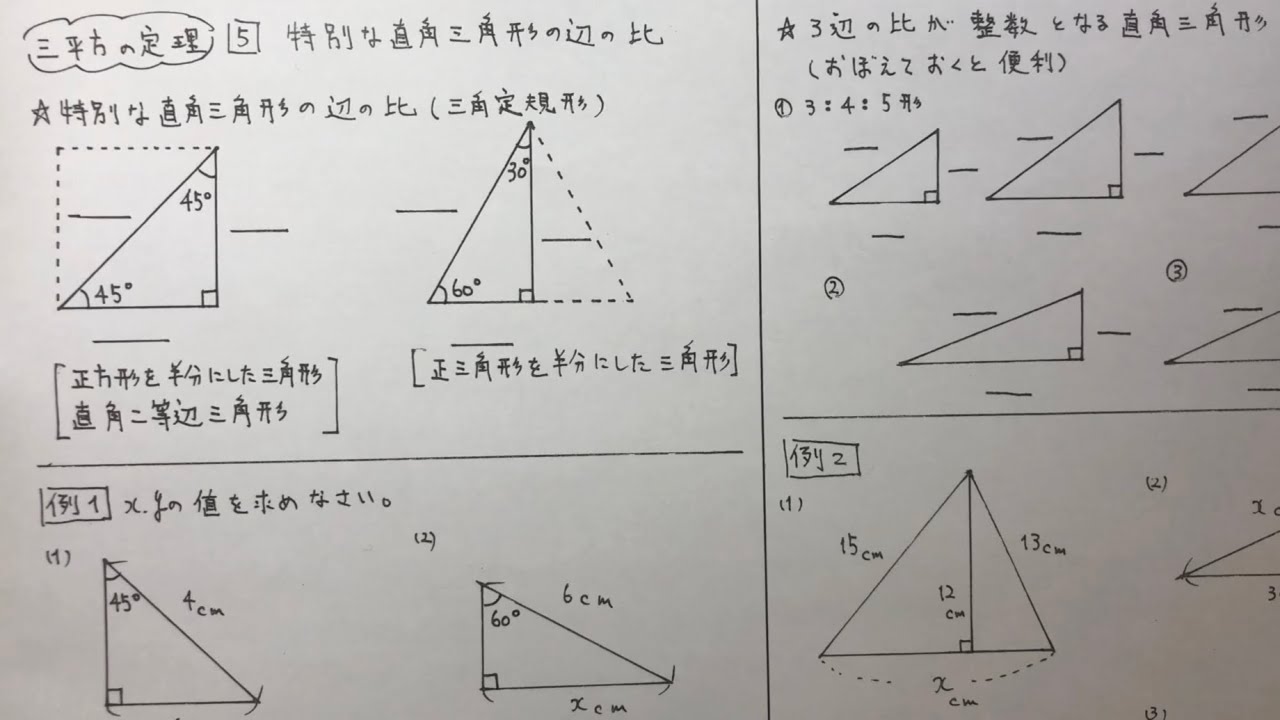
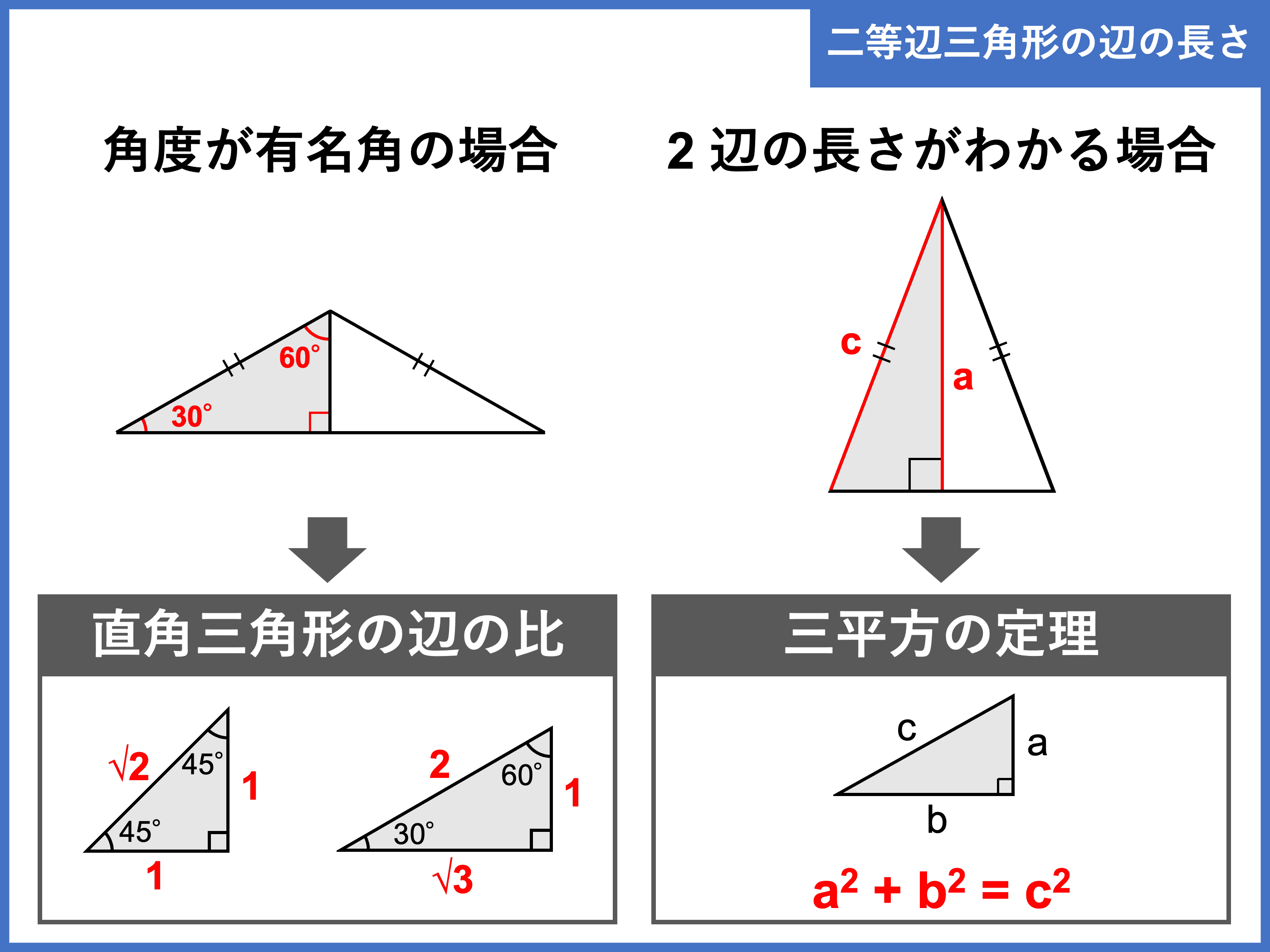
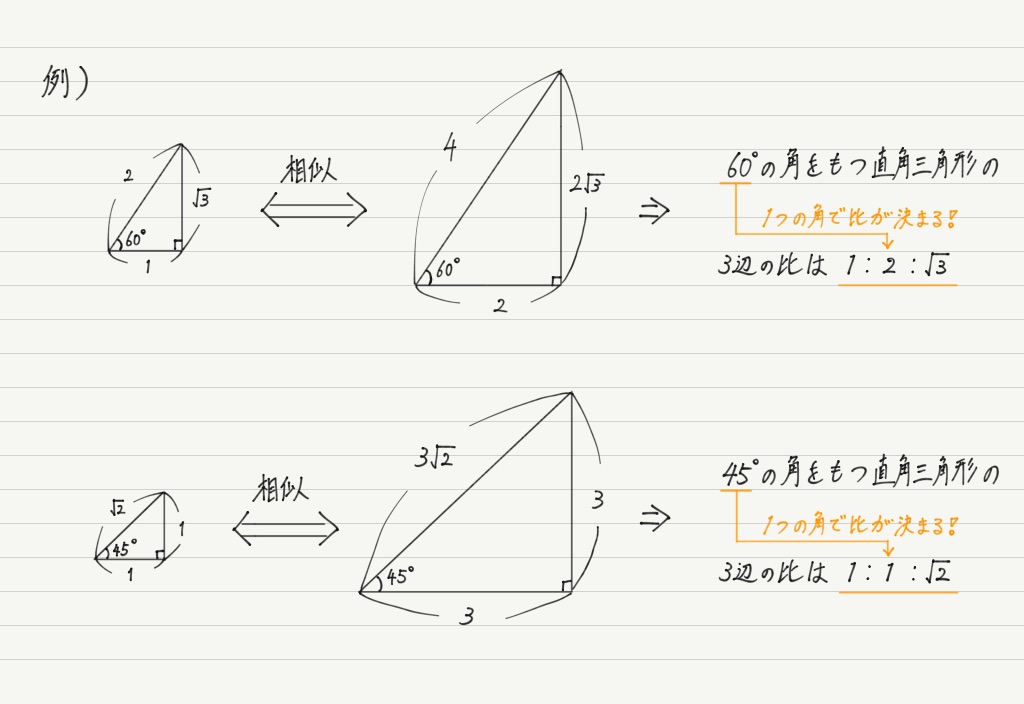
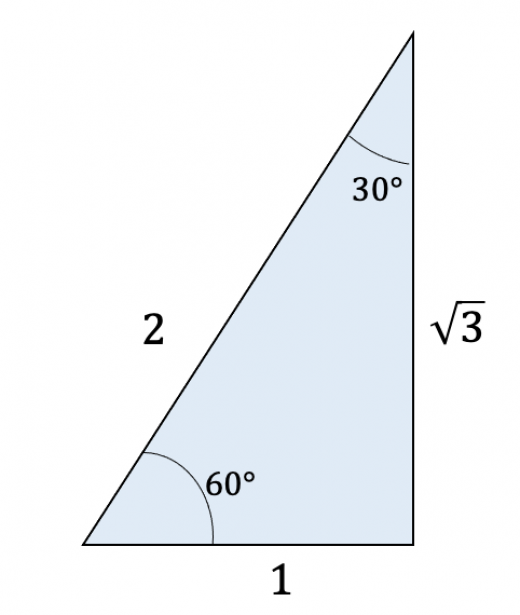
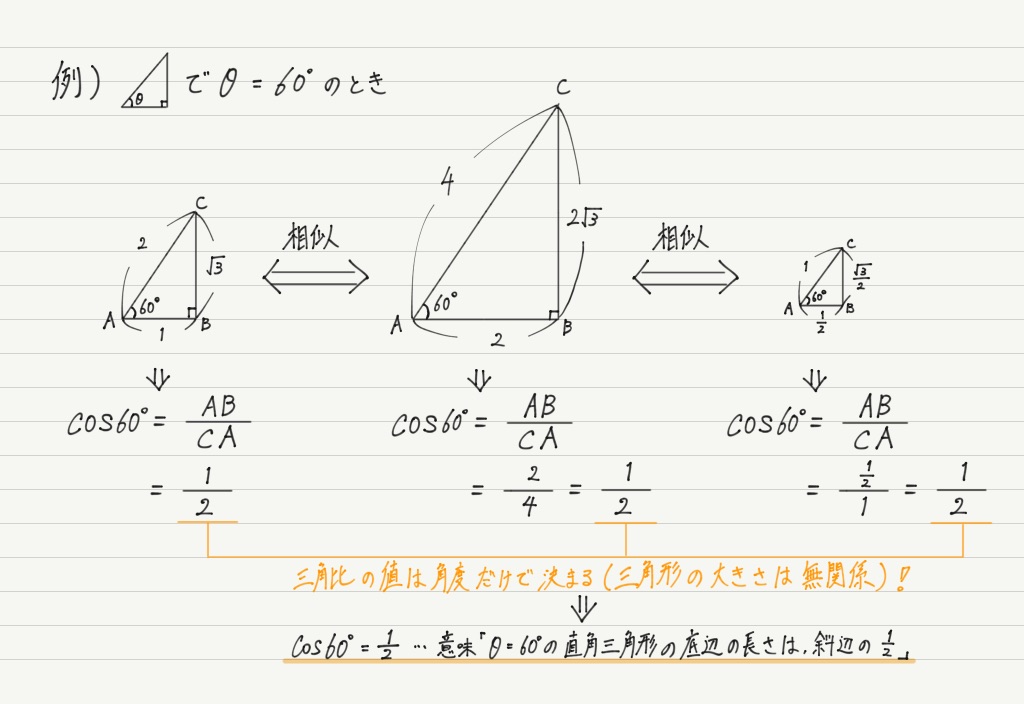
三角形 角度の比 辺の比-これらの角を持つ直角三角形には、特別な辺の比がありましたね。 この比を覚えておくだけで 実際の長さを調べくことなく三角比の値を求めることができます。 具体的には以下のようになります。 今後の問題では、30°、45°、60°の三角比を使って展開対応する辺はabとde・bcとef・acとdfになりますが、これらの比はすべて12となります。このような相似な図形における辺の長さの比のことを 相似比 (そうじひ)と言います。 相似比を求める問題としては以下のような問題があります。
直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典
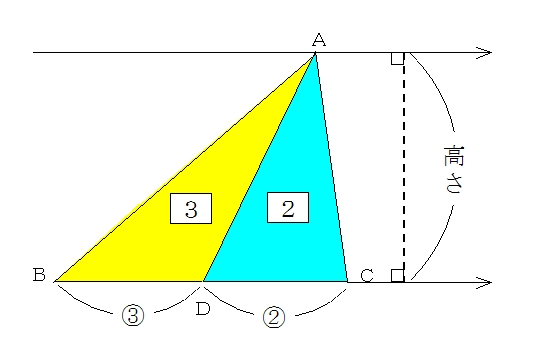
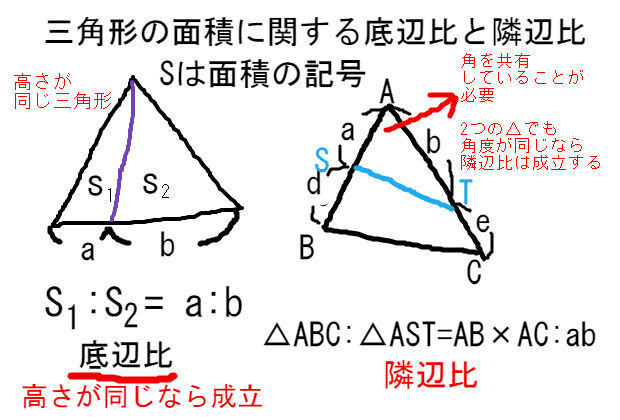
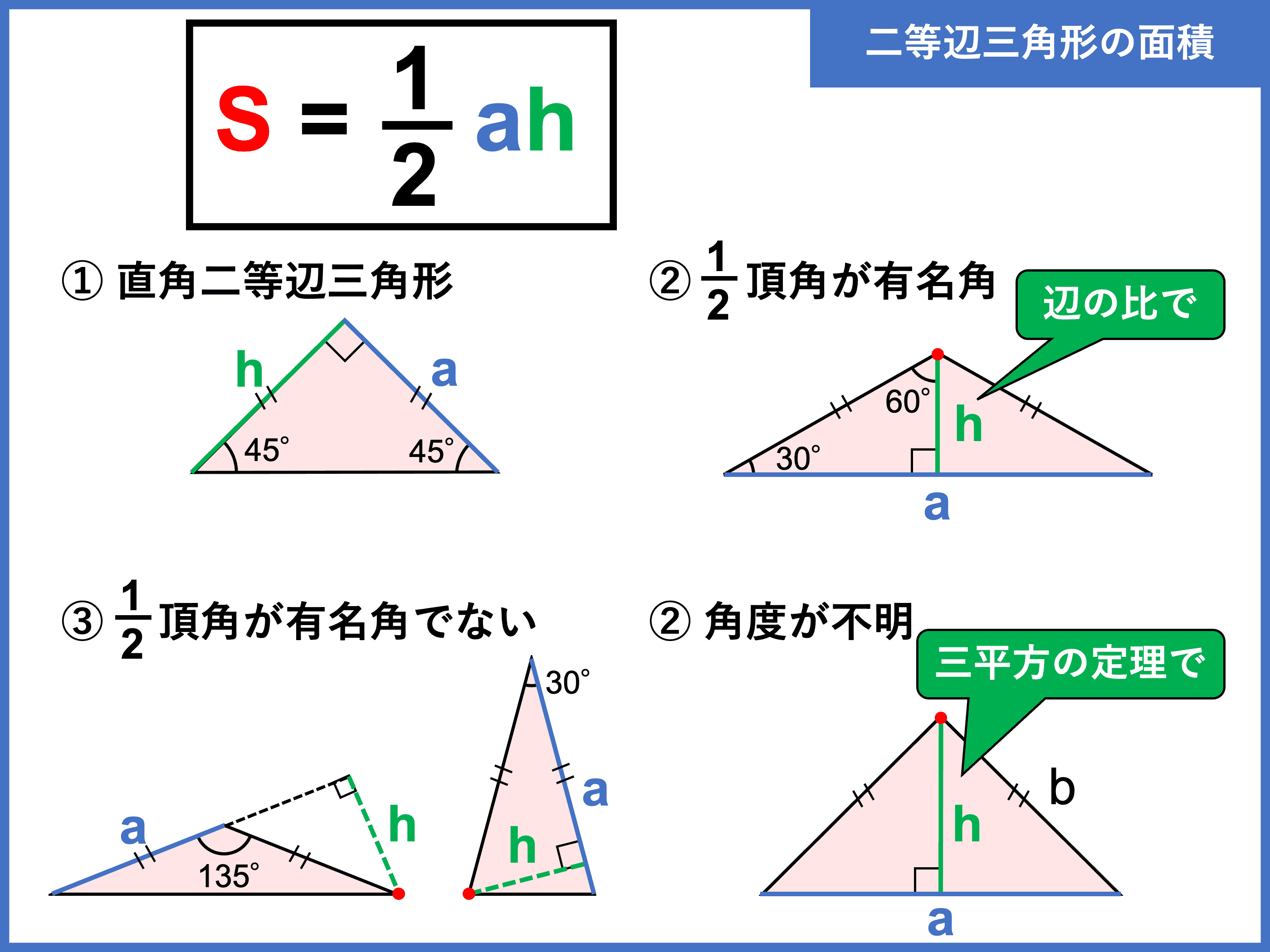
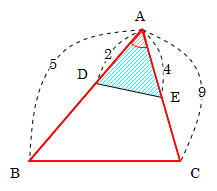
A b c m n abcの2辺ab, acの中点をそれぞれm, nとすると mn//bc, mn= 1 2 bcとなる。 定理の証明 amnと abcにおいて ∠aは共通(1) mはabの中点なのでamab=12 nはacの中点なのでanac=12 よってamab=anac=12(2) (1),(2)から2組の辺の比とその間の角がそれぞれ等しいので amn∽ abc次の図の abcと adeのように,1つの角(∠a)が共有されている2つの三角形の面積比について考えます。 となり,1つの角を共有する2つの三角形の面積比は,その共有する角をはさむ2辺の積の比と等しくなります。 正弦定理を使った場合の解の絞り込みに使えるのが、今回の「 三角形の辺と角の関係 」です。 角の大きさが大きい ほど、それに対する辺の大きさも大きくなる ことから、 $~\sin{A}=\displaystyle \frac{\sqrt{3}}{2}~$を満たす$~A~$を、次のように問題を解き切ることが
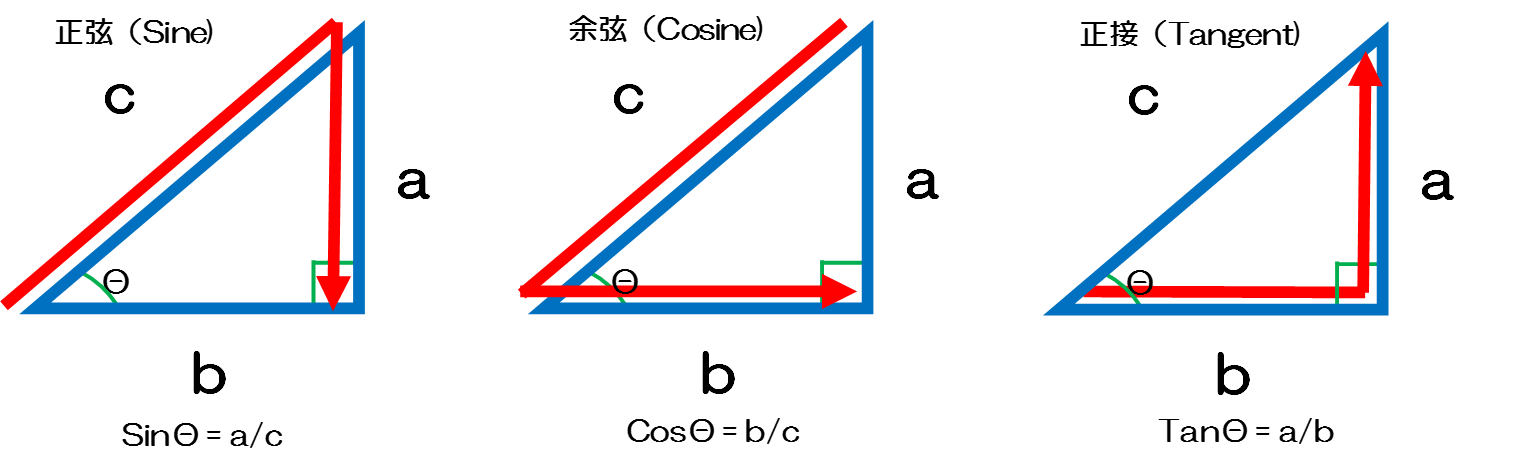
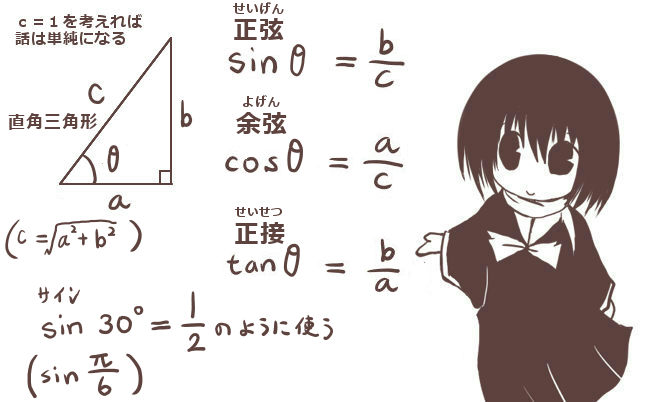
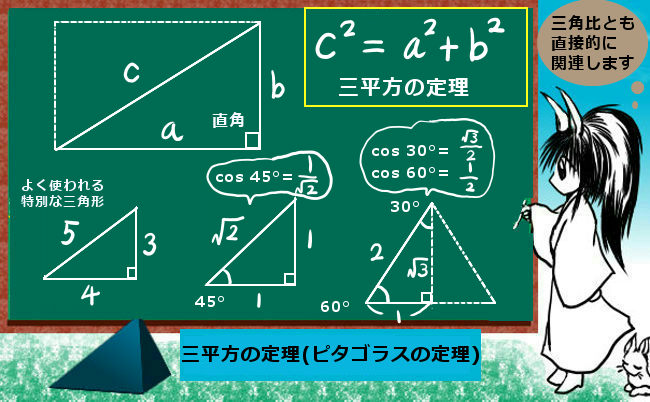
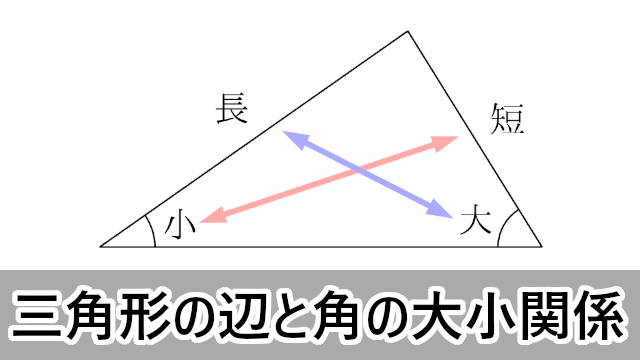
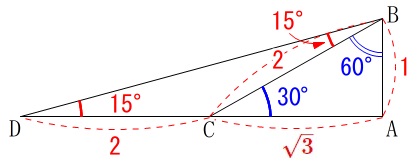
まず覚えておいておくべき直角三角形の辺の比は、 12√3 だよ。 この辺の比になる直角三角形の角度は、 30° 60° 90° になってるんだ。 例えば、次の直角三角形ABCがあったとして、辺BCの長さが2cmだったとしよう。辺の長さ、角度の関係 鋭角の三角比(えいかくのさんかくひ)とは、直角三角形の斜辺、高さ、底辺の比率と角度の関係を表したものです。 下図をみてください。 斜辺Aと底辺Bのなす鋭角をθ、高さをCとします このとき鋭角の三角比は下記のように表し 90度以下の範囲では、角度が大きくなると単位円周上の点の y 座標も大きくなる、ということを使っています(参考:基本よく出る0度から180度までの三角比の値)。 ここで証明したことは他の角・辺についても成り立つので、角の大小関係と辺の大小関係が一致することがわかり
三角形 角度の比 辺の比のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  |  |
 |  |  |
「三角形 角度の比 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三角形 角度の比 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三角形 角度の比 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
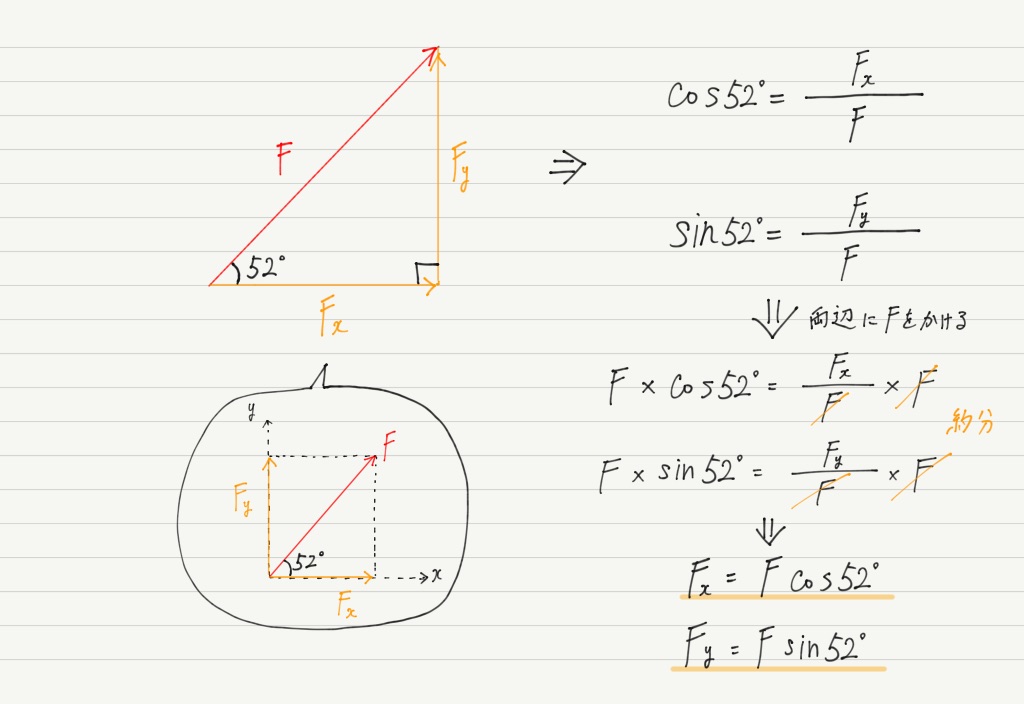 |  |  |
 |  |  |
「三角形 角度の比 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「三角形 角度の比 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
「三角形 角度の比 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三角形 角度の比 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「三角形 角度の比 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「三角形 角度の比 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「三角形 角度の比 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | 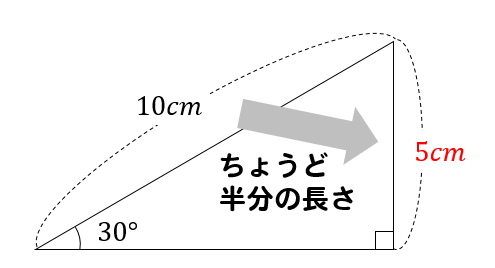 |
「三角形 角度の比 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |
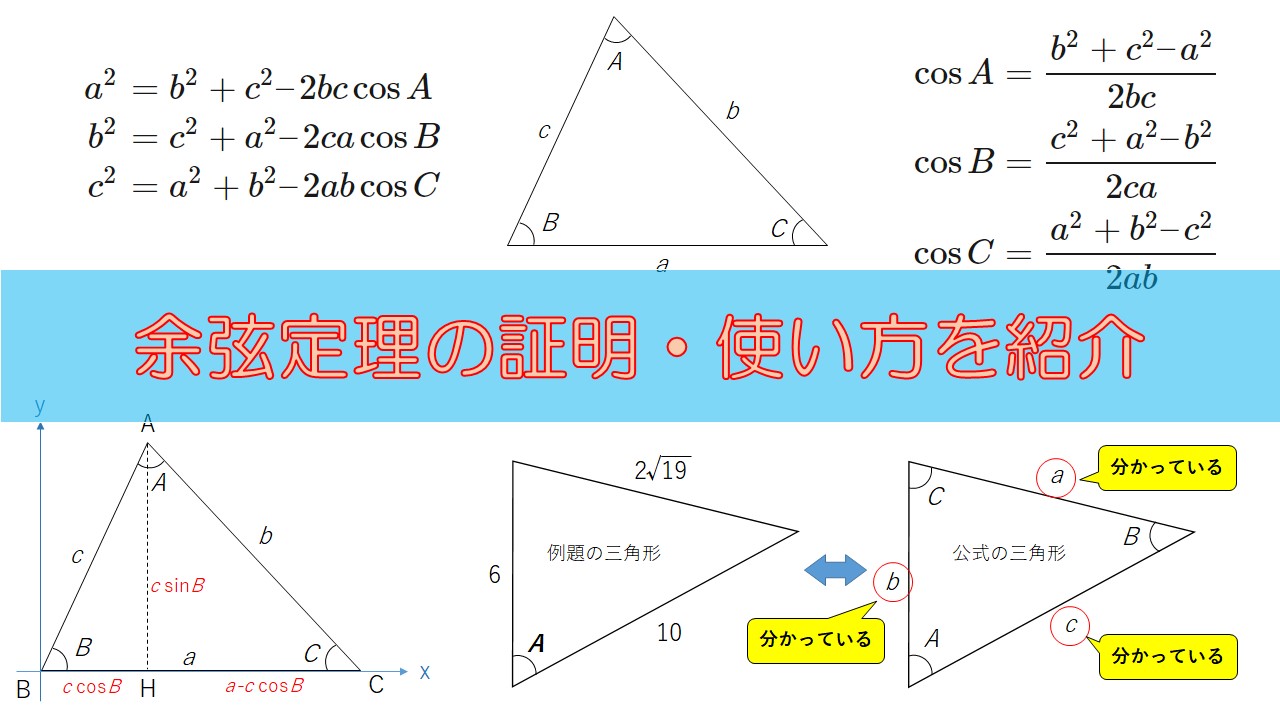
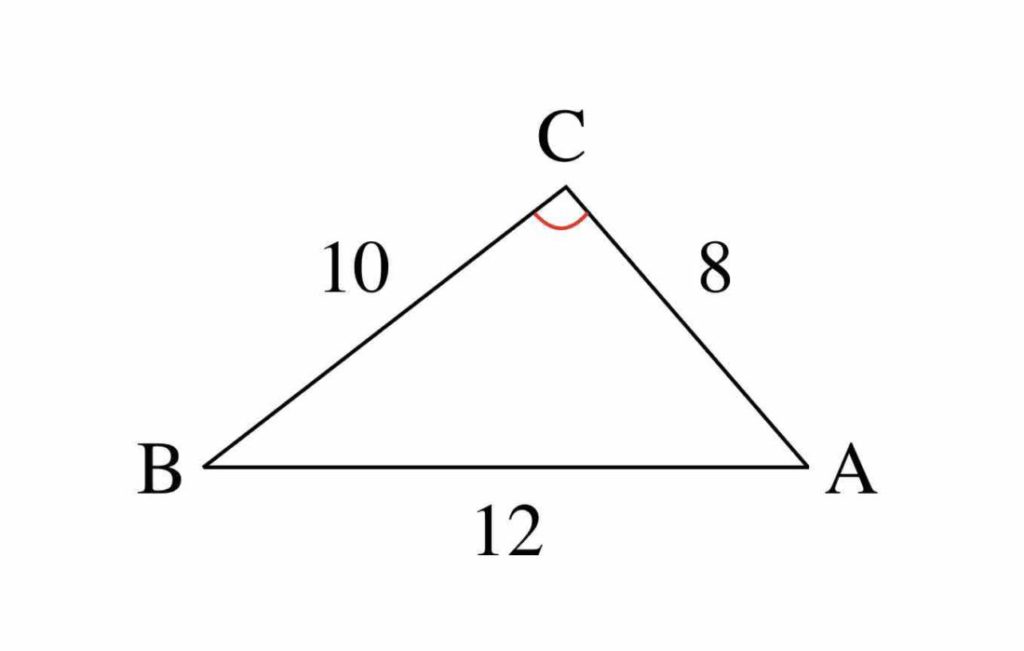
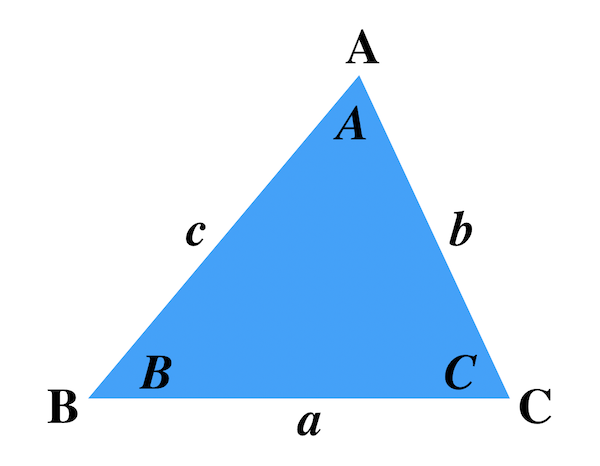
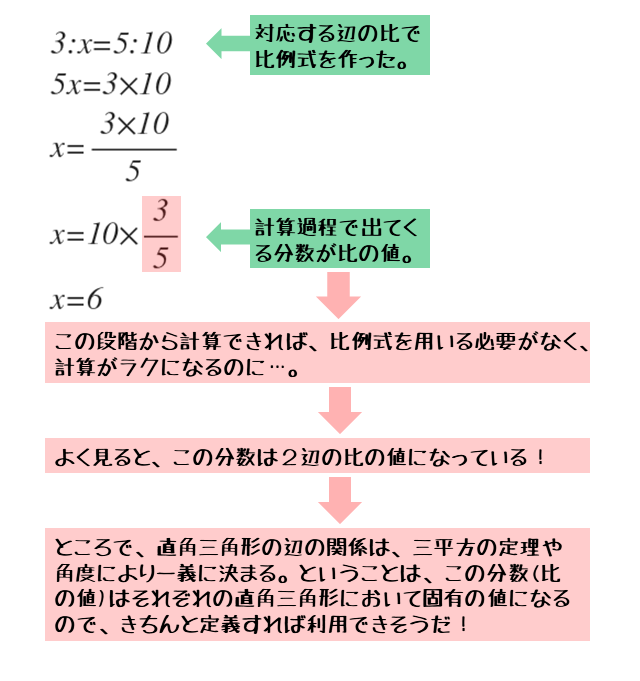
今度は、正弦定理を利用して角度を求めていきます。 三角比の方程式の解き方を思い出しましょう。 今回は、角度の範囲について注意が必要です。 解答 正弦定理より であるため、 ここで A = 60º より 0º < B < 180º A = 1º であるため B = 45º また C 正弦定理は、辺の比と sin sin の比が一致することを表している、と見ることもできるわけですね。 あとは、 標準余弦定理と比 と流れは同じです。 正の数 k を用いて、 a = 13k a = 13 k, b = 8k b = 8 k, c = 7k c = 7 k と書けます。 余弦定理から A = ( 8 k) 2 ( 7 k
Incoming Term: 角度の比 辺の比, 三角形 角度の比 辺の比,




0 件のコメント:
コメントを投稿