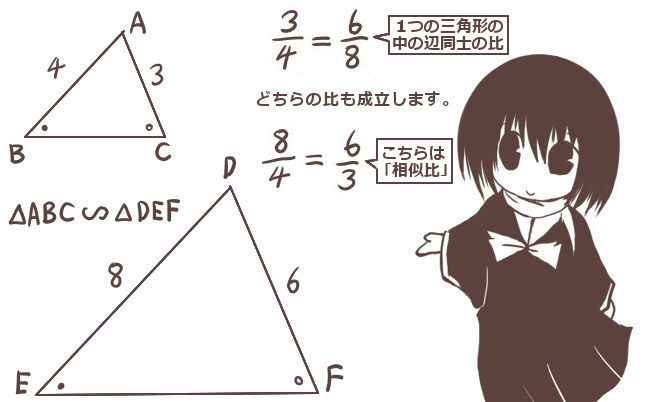
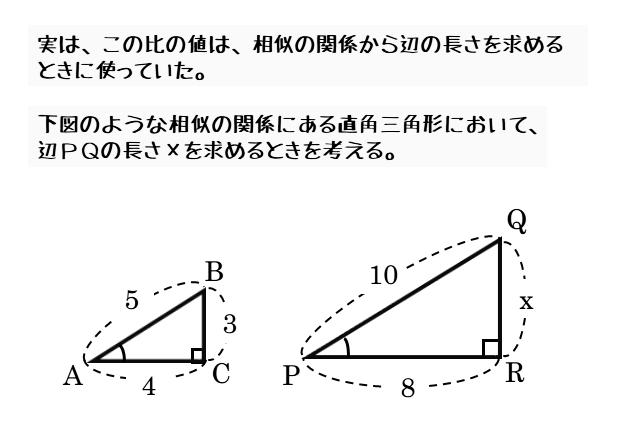
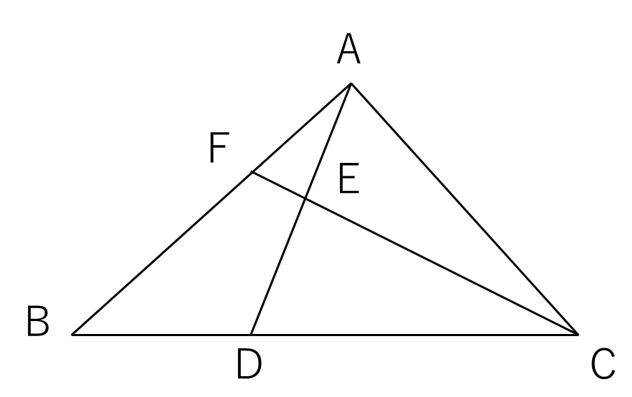
三角比 ここではまず, 弧度法 という角度の表現方法について述べておくその後, 直角三角形の2辺の比を利用して 三角比 という概念を導入する 三角比は, 力の合成・分解 というものと密接に関わっており, 学校教育においても数学より先に物理で出くわす三角形と比 三角形と比 三角形の一辺に平行な直線をひいた時にできる線分の比 について考えていこう。 辺AB を 4等分 するように 点D、E、F をおいてある。 直線は 3点 から 辺BC に平行になるようひいてあるよ。 AD:DE:EF:FB=1:1:1:1 となっている 比の値を意識することはなかったでしょうが、計算の中に 比の値 、つまり 三角比 が登場していたことは確かです。 ここから分かることは、 相似の関係にある直角三角形の辺の長さは、 比の値 を使えば求めることができる ということです。 察しの良い人なら、三角比から得られるメ

特別な直角三角形の辺の比 無料で使える中学学習プリント
比の計算 三角形
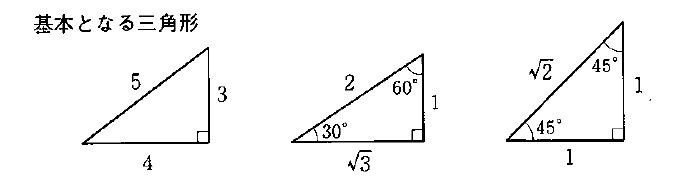
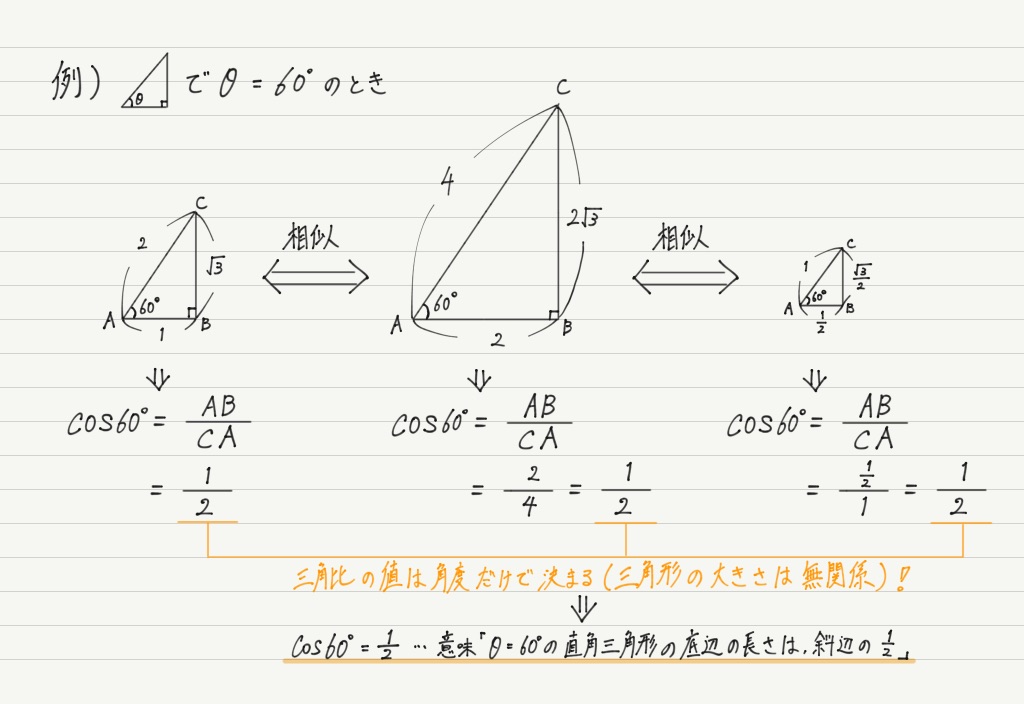
比の計算 三角形-比が表として (あるいは関数電卓の計算結果として )与えられている場合,直角三角形ならば, 三角形の解沵に必要な要素間の関係式がわかっていると考えていい。相似な三角形の辺の比は等しいので、30°、60°、90°の直角三角形であれば、その3辺の比は $12\sqrt{3}$ であることが分かります。 以上が、代表的な 2 つの直角三角形の辺の比と、それを三平方の定理から求める手順です。



算数 テーマ別 ポイント集 平面図形 10 14 中学受験の勉強法 偏差値アップの学習法
そこで,図の青い三角形に着目すると,1つの内角が60°の直角三角形ですから辺の比が1:2: であることがわかります。 だから,斜辺を1とすると,それぞれの辺の長さは, となります。 また,点Pのある場所で,そのx ,y の符号をとらえます。直角三角形计算器 如果给出足够的几何属性, 直角三角形计算器 就能自动补全直角三角形的所有属性,如面积,周长,边和角度。 直角三角形是一个具有三个顶点(角)和三个边(边)的多边形,其中两条边以直角相交。 直角三角形 维基百科页面正弦定理から,三角形の辺の長さを求める計算について ABCにおいてa = 3 ,A = 60°,B = 45°のときbを求めよ。 という問題がありますが, これを定理にあてはめていって, b = 3 / sin60°× sin45° まではつくれるんですが,そこから (3 ÷ √3/2 ) × 1/√2= 6/√6=√6 というのになるのが,意味がわかりま
中点連結定理 a b c m n abcの2辺ab, acの中点をそれぞれm, nとすると mn//bc, mn= 1 2 bcとなる。 定理の証明 amnと abcにおいて ∠aは共通(1) mはabの中点なのでamab=12 nはacの中点なのでanac=12 よってamab=anac=12(2)これらは三角比を用いた定理であり、任意の三角形について成立する定理である。 正弦定理 最初に正弦定理を使う。三角形の辺の長さがa,b,cと与えられ、相対する角の大きさがA,B,Cと与えられるとき三角形の辺の長さを求めるときの三角比の値 下の図のxの値を求めよ。 これを解こうとすると,sin45°,sin60°という三角比が出てきました。 定義では,「直角三角形」だけで考えるとありまし
右図6の凹四角形 abcd は三角形 abd から三角形 bdc を取り除いたものだから、その面積は − =12−6=6 になります。 (4) 縮尺図を用いて表しているときに実際の図形の面積を求めるには、各辺の実際の長さを求めてから計算しなければなりません。三角比の計算に よる問題解決を する。 三角比と角度の 関係を理解す る。 三角比表の見方 を理解する。 数学的考察・処 理の場面 図式化して三角 比に表現でき る。 計算して、問題 解決する。 三角比(辺の長さの比)を用いて計 算する。 測量では、三角比( (サイン)、 (コサイン)、 (タンジェント))というものを使用して点と点との間の距離を求めます。 日常の生活や仕事などでは2点間の距離を測ることがよくあり



図形と計量 三角比の定義について 日々是鍛錬 ひびこれたんれん



3
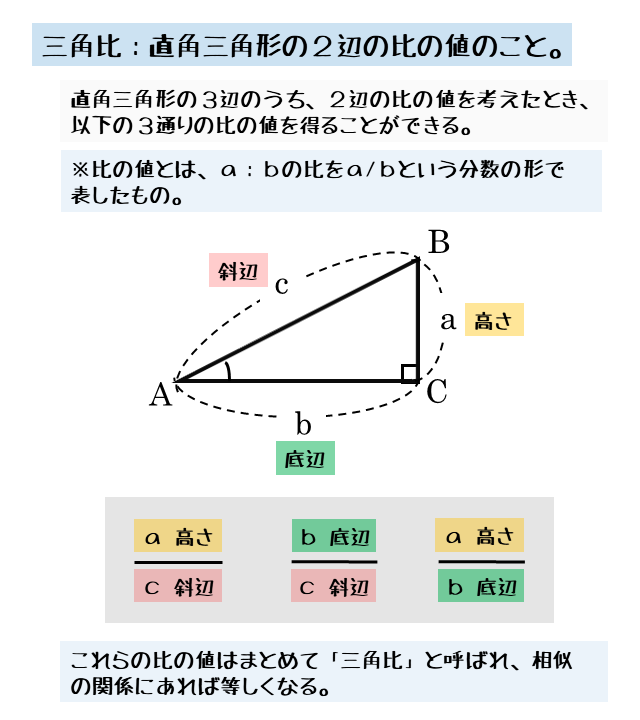
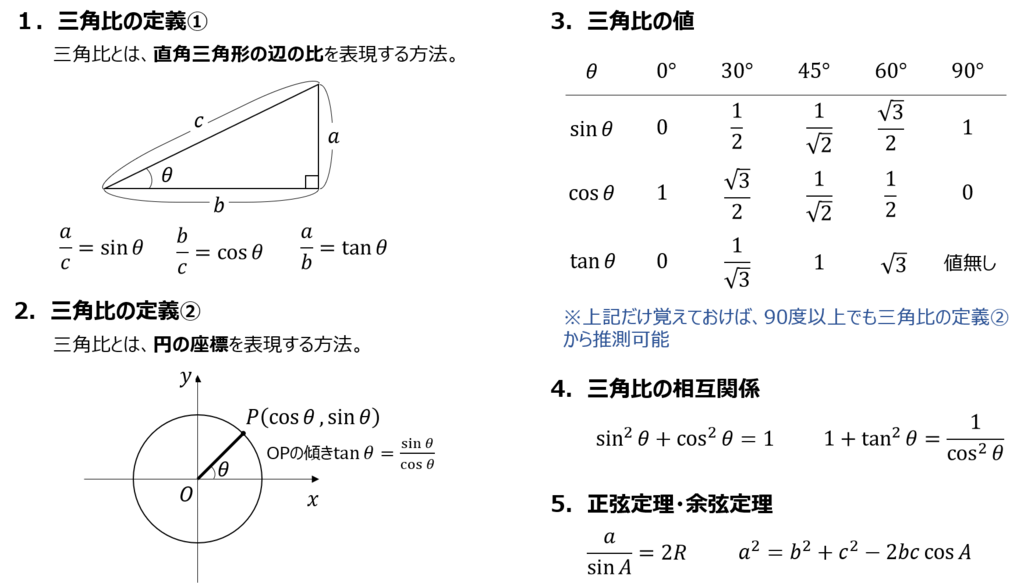
これは簡単、AC:CB=2:1ですね。 線分の比では、AC:CBというただ1つの比を求めればよかったのに対し、 三角形の面積比は2つの比 を扱います。関数を使用してcsc(コセカント)の数値を出してみよう! コセカントの計算1つ目角度30度のcsc コセカントの計算2つ目!角度45度のcsc エクセルで特殊な三角比計算!cosecを求めてみようまとめ三角比の計算式を下記に示します。三角比は三角形の大きさとは無関係で、角度のみが関係する値です。 ・sinθ=高さ/斜辺 ・cosθ=底辺/斜辺 ・tanθ=高さ/底辺 よって、直角三角形の角度が分かれば、三角比を用いて「辺の長さ」を求めることが可能です。



目指せ 建築士 濱崎塾 カリスマ講師の学習アドバイス 日建学院
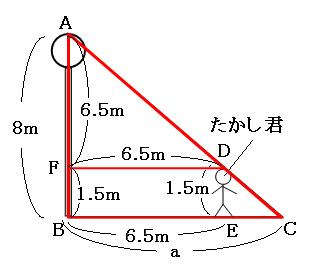



影の長さを求める相似問題の解き方を解説 出題パターンは2つ
正三角形を半分にした形って覚えてもらえればいいかな。 中学数学の問題では3秒に一回ぐらい使う直角三角形の辺の比だから、 確実に覚えておこう。 比その2「11√2」 次の直角三角形の辺の比は、 1 1 √2 だよ。 これは直角三角形の角度がそれぞれ★無料の中学メルマガ講座★毎週、問題と動画講義をお届け! 勉強の習慣が身につく わかることが増えて楽しい 誰でも自由に学べる今すぐ無料 三角形に限らず、どのような相似な図形においても、面積比は相似比の \(\bf{2}\) 乗となります。 相似の計算問題 それでは、ここまでに学んだ知識を活かして相似の計算問題に挑戦してみましょう。 計算問題①「三角形の相似比を求める」




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
直角三角形 110 /2件 表示件数 5 10 30 50 100 0 1 1245 60歳以上 / その他 / 非常に役に立った / 直角三角形の辺の比である三角比を扱うことで、いろんなことがラクになるんだ。 図形の辺の長さを求めたり、面積を求めたり 普通の計算では、とっても面倒なものをサクッと計算してくれるんだ。 とってもありがたい存在だよね! なので、そんな三角三角比を求められるようにしておきましょう。 30° 45° √3 1 1つの角が 30° である直角三角形の辺の比は 1∶2∶√3 となっているので,sin30°= また,1つの角が 60° である直角三角形の辺の比も同様なの




相似 台形と面積比の問題を徹底解説 数スタ
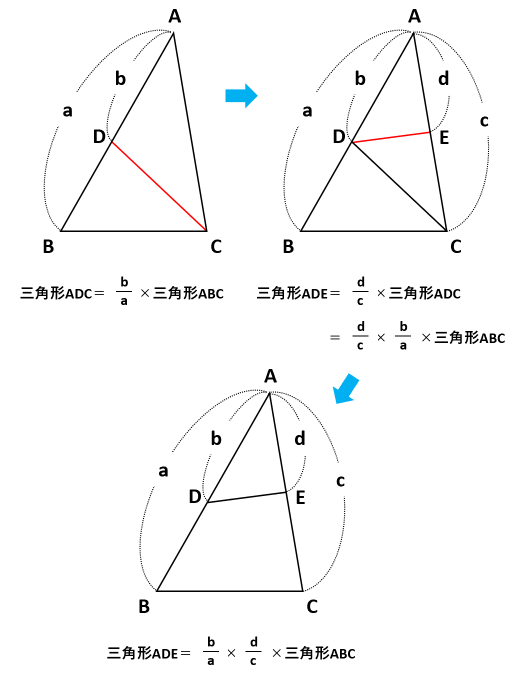



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ
メネラウスの定理,チェバの定理 → 携帯版は別頁 面積の比 → 印刷用PDF版は別頁 1 2つの三角形の高さが等しいときは,面積の比は底辺の長さの比に等しい. ※ 辺 BC の長さを BC と書く.文字式の計算として B と C を掛けているわけではない. BD も辺の 三角形の面積を外接円の半径を使って求める 問43⊿ABCの3辺をa,b,c,面積をS,・・・外接円の半径をRとすると、次の関係が成立することを示しなさい。 この問題は、上の式のように、正弦定理を使って計算できます。 答えをおぼえるよりは、この三角形の面積のポイントは!・三角形の面積 = 1 / 2 × (2つの辺) × sin(挟む角)前の動画形状決定~演習https//youtube




黄金三角形による18 シリーズの三角比 おいしい数学



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典
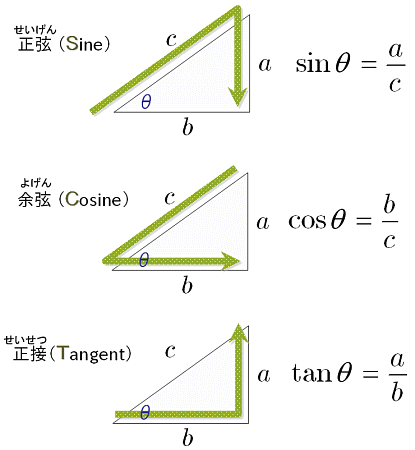
< 三角比1 > 右の図のように,直角三角形の鋭角のひとつをθとする。 斜辺の長さをr,他の辺の長さをx,y とするとき, y r, x r, y x, の値は,三角形の大きさに関係なく,角θの大きさだけで決まる。 これらを,それぞれθの 正弦(sine), 余弦(cosine), 正接(tangent) 三角比の定義 まず、三角比とは何かというと 直角三角形 における、ある辺とある辺の 比 です。そして、この比は三角形の内角により変化していく( ここについてはあまり深く考えないほうがいいかもしれません、三角比をとりあえず受け入れるとわかってきます )ので、それを次の三角形计算器 如果给出足够的几何属性, 任意三角形计算器 就能自动补全任意三角形的所有属性,例如面积,周长,边和角度。 三角形是具有三个顶点(角)和三条边(边)的多边形。 任意三角形 维基百



面積分割




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
「縦の長さ x 横の長さ = 面積」ということですね。




中学数学 相似比の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
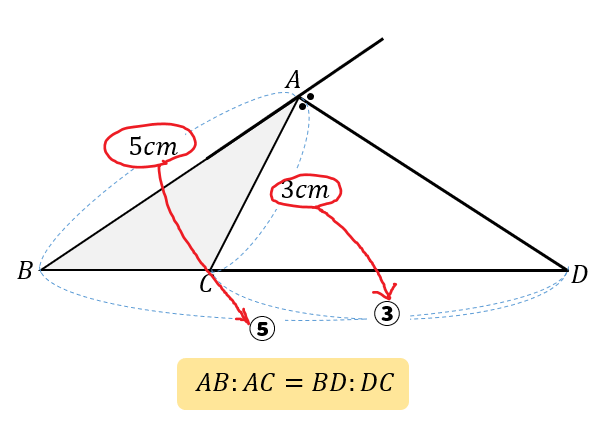



サクッと解説 角の二等分線と比の特徴となぜ について 数スタ




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト




無料 中3数学 基本解説 解答プリント 334 三平方の定理2 比の利用



1




中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su
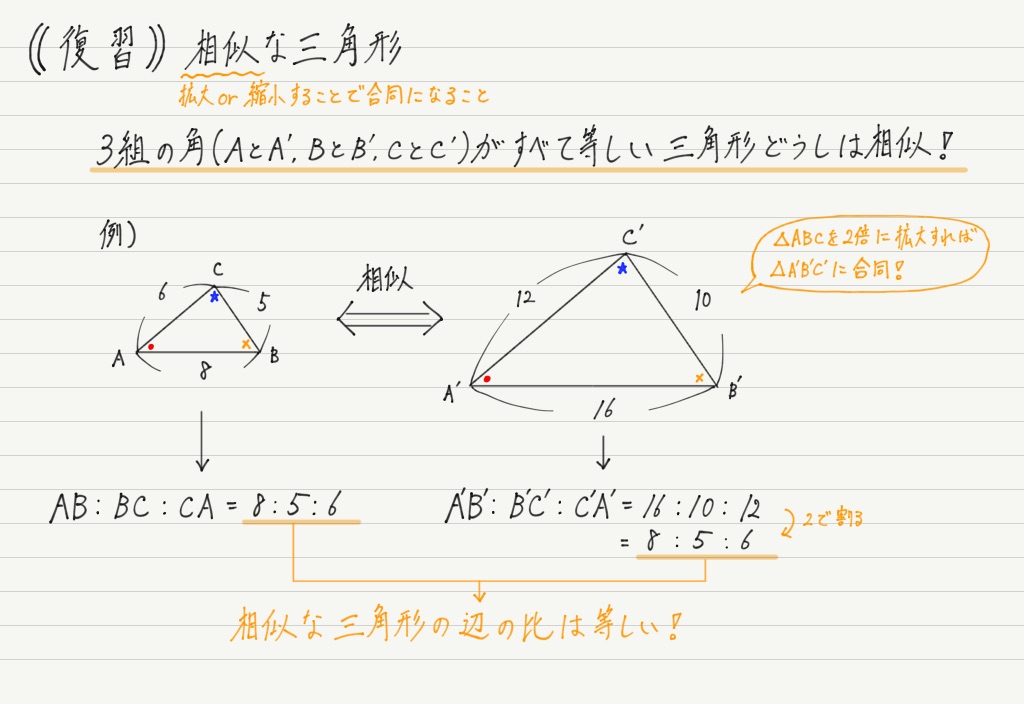



三角比と三角関数 高校物理をあきらめる前に 高校物理をあきらめる前に




黄金三角形による18 シリーズの三角比 おいしい数学




数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



算数 テーマ別 ポイント集 平面図形 10 14 中学受験の勉強法 偏差値アップの学習法



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典




正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典




特別な直角三角形の辺の比 無料で使える中学学習プリント




底辺と高さから角度と斜辺を計算 高精度計算サイト



辺の比と面積比 等角三角形 富士山型 Next Stageのブログ




直角三角形の角から垂線を引いたときの底辺の比の問題 の裏ワザ 大阪のプロ家庭教師が できない を できる に変える




三角定規の直角三角形のときは 比の計算で簡単に求めよう 中学や高校の数学の計算問題
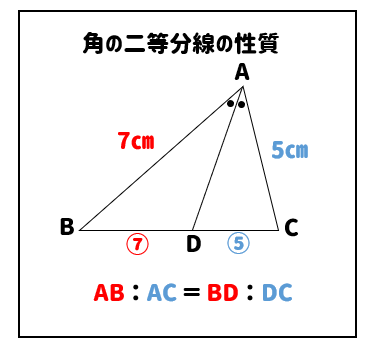



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ



三平方の定理から円周率を計算してみる Yamav1 02bのブログ




ヘロンの公式で三角形の面積を求める 三辺の長さがわかっているときはコレ 数学の面白いこと 役に立つことをまとめたサイト




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




数学 中3 49 平行線と線分の比 基本編 Youtube
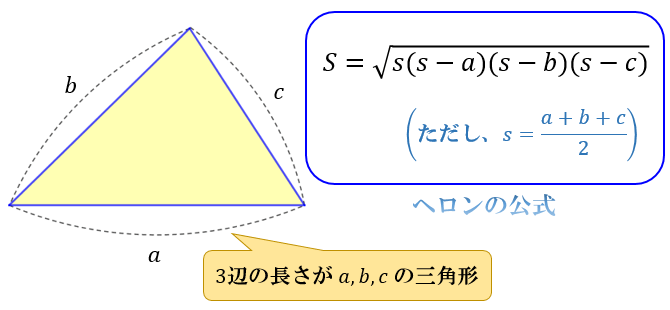



ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ



直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora




平面図形の苦手を解消 三角形の面積比 基本編
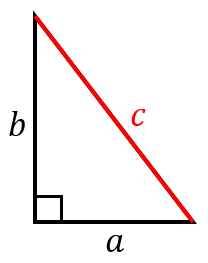



直角三角形の辺の長さの求め方と計算ツール 具体例で学ぶ数学
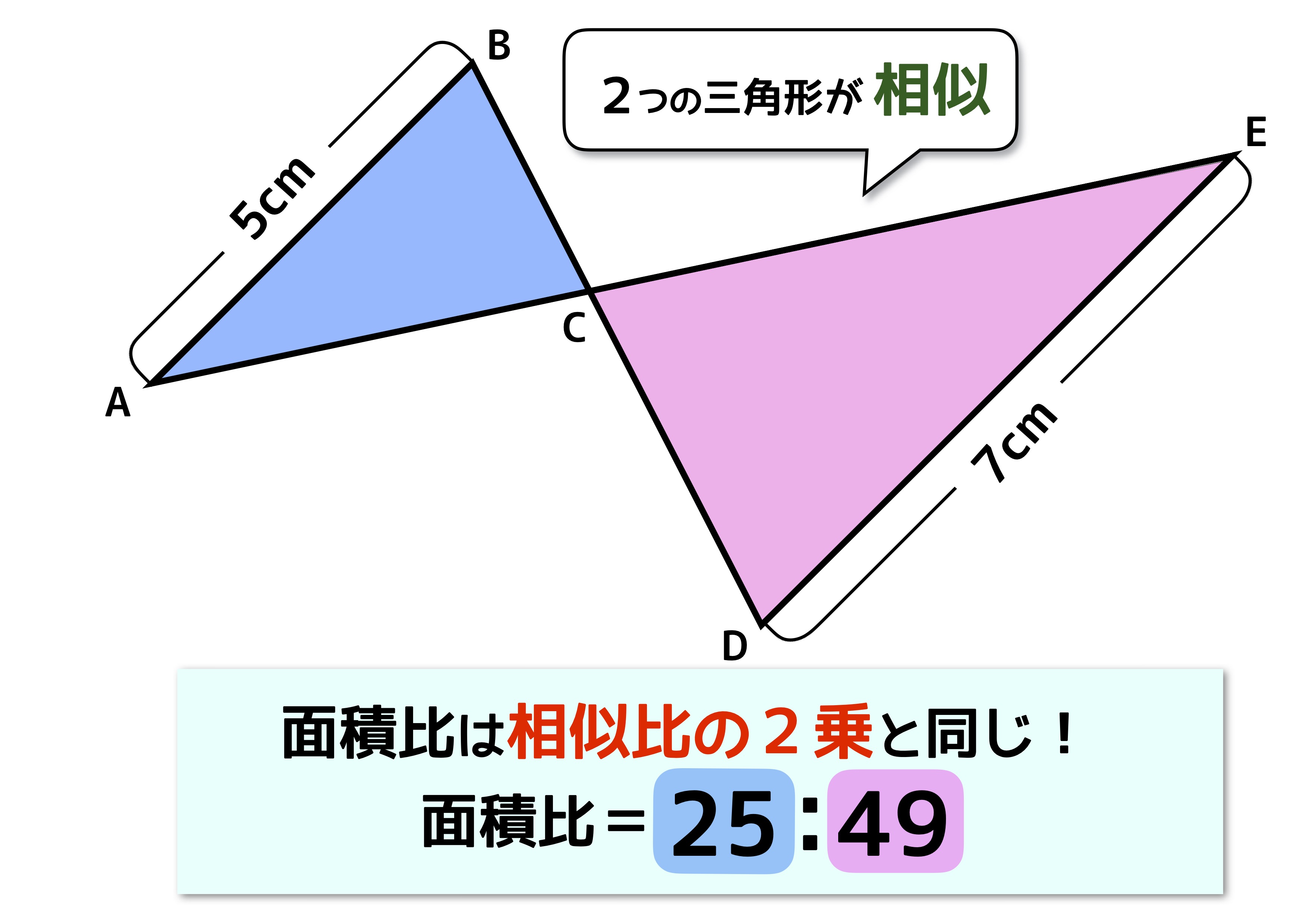



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




三角比の値の求め方 数学苦手な人に向けて基本をイチから解説していくぞ 数スタ




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者



面積比とは 1分でわかる意味 公式と求め方 問題 三角形と四角形の関係



1
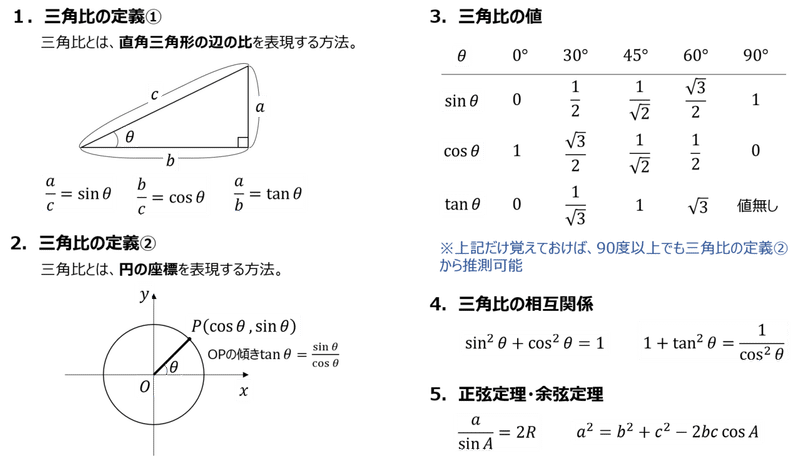



三角比は1時間で解けるようになる 箕輪 旭 Note



比の表し方と計算 中学から数学だいすき




平面図形の苦手を解消 三角形の面積比 基本編
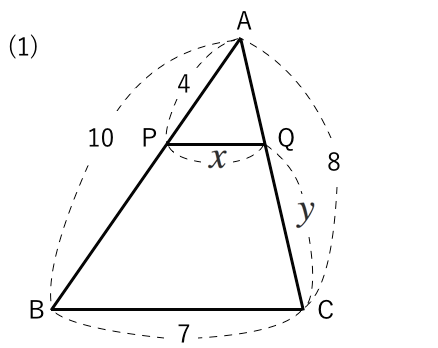



相似な図形 長さを求める 苦手な数学を簡単に



三角形の相似 理数系無料オンライン学習 Kori




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube




黄金三角形による18 シリーズの三角比 おいしい数学
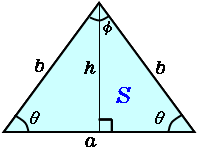



二等辺三角形 高精度計算サイト




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三角比 30 45 60 もう一度やり直しの算数 数学



図形と計量 三角比の定義について 日々是鍛錬 ひびこれたんれん



2つの線分の交点の位置ベクトルや内分比を求める裏技 教師用
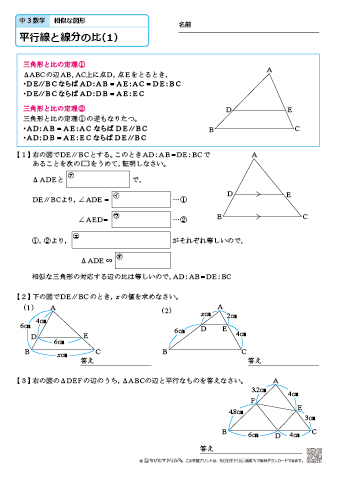



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




小学6年生 算数 10月 辺の比と面積の比 速さ 1 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ




三角形の面積比 数学の偏差値を上げて合格を目指す
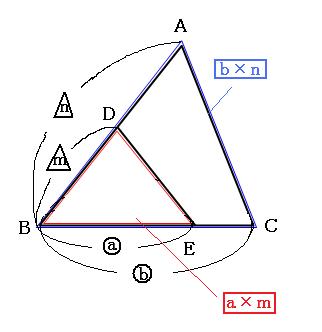



面積と辺の比の関係を解説 図形の面積と辺の比の関係はテントやドリルで面積を求める




高校入試対策数学 面積比に関する対策問題 Pikuu




高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月




平行線と線分の比 三角形の比の取り方を簡単な問題で覚えよう 中学や高校の数学の計算問題



正三角形の辺の比率は 1分でわかる値と計算方法 底辺と高さの比




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学
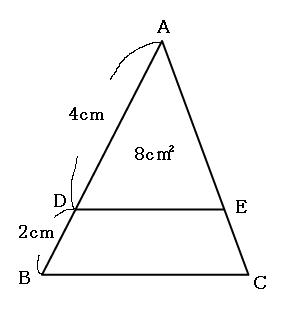



相似比と面積比と体積比の関係を解説 公式を使って面積や体積を求めよう




力の分解 三角比編 高校物理をあきらめる前に 高校物理をあきらめる前に




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生




三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ




平面図形をマスター 三角形の面積比 応用編その3



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典




高校数学 数 76 三角比 基本編 Youtube




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比




余弦定理で角度を求める方法 数学の星



面積分割




平面図形の苦手を解消 三角形の面積比 基本編
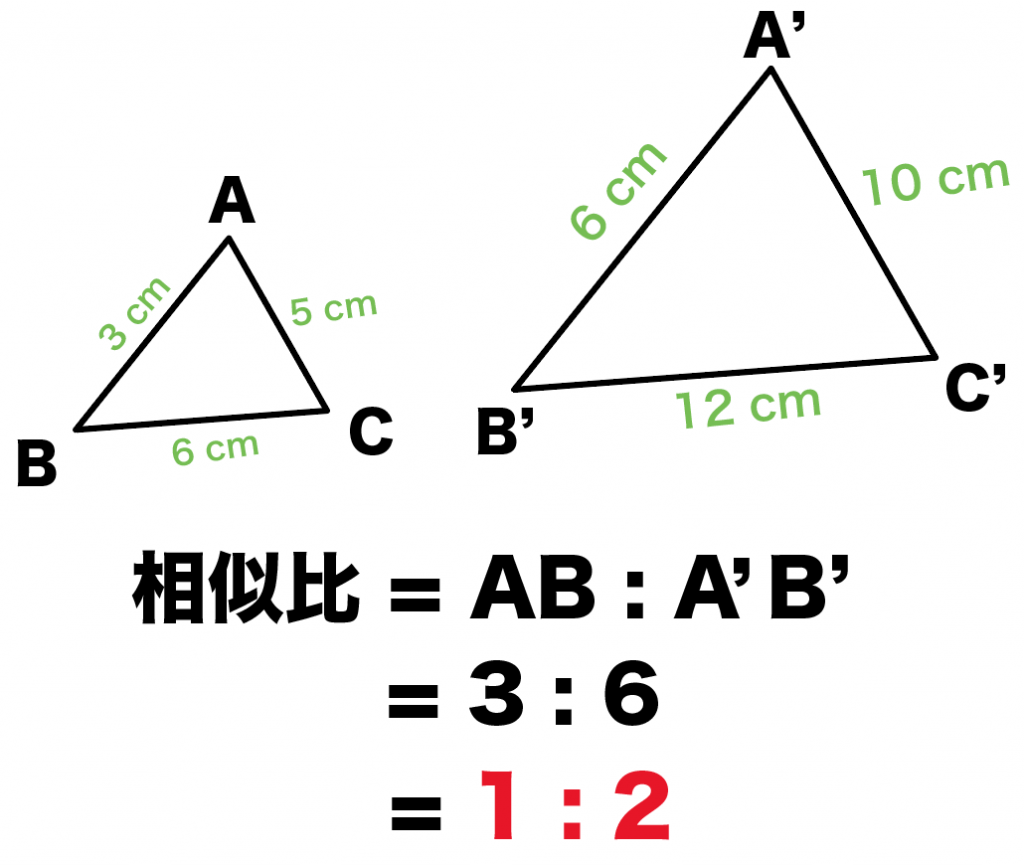



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく
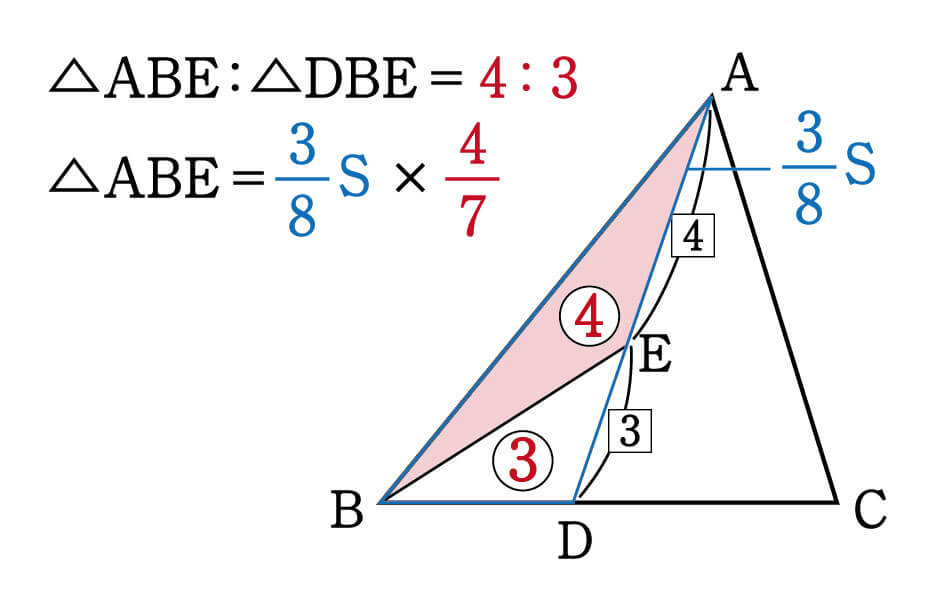



数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




中点連結定理と相似 定理の逆や平行四辺形の証明 応用問題の解き方 リョースケ大学




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三平方の定理 覚えること 三角定規 苦手な数学を簡単に




中3 三角形の相似 円錐の体積比 日本語版 Youtube




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



三角比 三角比とはなにか 大人が学び直す数学




Nitter




中学数学 相似比の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



Studydoctor相似比と面積の計算 中学3年数学 Studydoctor




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



三角比と三角関数 高校物理をあきらめる前に 高校物理をあきらめる前に




相似な図形の面積比の問題 相似比を出してから二乗しよう 中学や高校の数学の計算問題




三角比を使って三角形の面積を求める方法 数学i By Okボーイ マナペディア



1



相似比とは 1分でわかる意味 面積比 四角形と三角形の問題




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー



三角比は1時間で解けるようになる 外資系コンサルタントが主夫になったら



三角形の面積比をてんびんで解く 中学受験プロ講師ブログ



Studydoctor相似な三角形の辺の比 中3数学 Studydoctor




3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿